数据结构与算法教程，数据结构C语言版教程！（第五部分、数组和广义表详解）二

?第五部分、数组和广义表详解

数组和广义表，都用于存储逻辑关系为“一对一”的数据。

数组存储结构，99% 的编程语言都包含的存储结构，用于存储不可再分的单一数据；而广义表不同，它还可以存储子广义表。

本章重点从矩阵的角度讨论二维数组的存储，同时讲解广义表的存储结构以及有关其广度和深度的算法实现。

三、矩阵（稀疏矩阵）压缩存储（3种方式）

数据结构中，提供针对某些特殊矩阵的压缩存储结构。

这里所说的特殊矩阵，主要分为以下两类：

• 含有大量相同数据元素的矩阵，比如对称矩阵；
• 含有大量 0 元素的矩阵，比如稀疏矩阵、上（下）三角矩阵；

针对以上两类矩阵，数据结构的压缩存储思想是：矩阵中的相同数据元素（包括元素 0）只存储一个。

1、对称矩阵

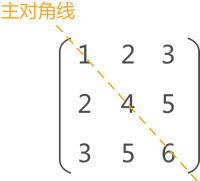
图 1 对称矩阵示意图

图 1 的矩阵中，数据元素沿主对角线对应相等，这类矩阵称为对称矩阵。

矩阵中有两条对角线，其中图 1 中的对角线称为主对角线，另一条从左下角到右上角的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。

结合数据结构压缩存储的思想，我们可以使用一维数组存储对称矩阵。由于矩阵中沿对角线两侧的数据相等，因此数组中只需存储对角线一侧（包含对角线）的数据即可。

对称矩阵的实现过程是，若存储下三角中的元素，只需将各元素所在的行标 i 和列标 j 代入下面的公式：

存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式：

最终求得的 k 值即为该元素存储到数组中的位置（矩阵中元素的行标和列标都从 1 开始）。

例如，在数组 skr[6] 中存储图 1 中的对称矩阵，则矩阵的压缩存储状态如图 3 所示（存储上三角和下三角的结果相同）：

图 3 对称矩阵的压缩存储示意图

注意，以上两个公式既是用来存储矩阵中元素的，也用来从数组中提取矩阵相应位置的元素。例如，如果想从图 3 中的数组提取矩阵中位于 (3,1) 处的元素，由于该元素位于下三角，需用下三角公式获取元素在数组中的位置，即：

结合图 3，数组下标为 3 的位置存储的是元素 3，与图 1 对应。

2、上（下）三角矩阵

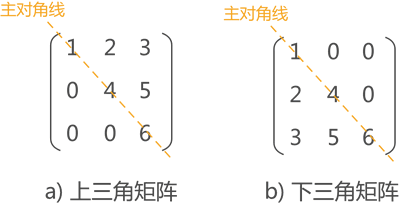
图 4 上(下)三角矩阵

如图 4 所示，主对角线下的数据元素全部相同的矩阵为上三角矩阵（图 4a)），主对角线上元素全部相同的矩阵为下三角矩阵（图 4b)）。

对于这类特殊的矩阵，压缩存储的方式是：上（下）三角矩阵采用对称矩阵的方式存储上（下）三角的数据（元素 0 不用存储）。

例如，压缩存储图 4a) 中的上三角矩阵，矩阵最终的存储状态同图 3 相同。因此可以得出这样一个结论，上(下)三角矩阵存储元素和提取元素的过程和对称矩阵相同。

3、稀疏矩阵

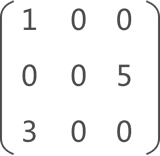
图 5 稀疏矩阵示意图

如图 5 所示，如果矩阵中分布有大量的元素 0，即非 0 元素非常少，这类矩阵称为稀疏矩阵。

压缩存储稀疏矩阵的方法是：只存储矩阵中的非 0 元素，与前面的存储方法不同，稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。

例如，存储图 5 中的稀疏矩阵，需存储以下信息：

• (1,1,1)：数据元素为 1，在矩阵中的位置为 (1,1)；
• (3,3,1)：数据元素为 3，在矩阵中的位置为 (3,1)；
• (5,2,3)：数据元素为 5，在矩阵中的位置为 (2,3)；
• 除此之外，还要存储矩阵的行数 3 和列数 3；

由此，可以成功存储一个稀疏矩阵。

注意，以上 3 种特殊矩阵的压缩存储，除了将数据元素存储起来，还要存储矩阵的行数值和列数值，具体的实现方式后续会介绍 3 种，本节仅需了解矩阵压缩存储的原理。

4、矩阵压缩存储的 3 种方式

对于以上 3 种特殊的矩阵，对阵矩阵和上下三角矩阵的实现方法是相同的，且实现过程比较容易，仅需套用上面给出的公式即可。

稀疏矩阵的压缩存储，数据结构提供有 3 种具体实现方式：

1. 三元组顺序表；
2. ?行逻辑链接的顺序表；
3. 十字链表；

稀疏矩阵的三种存储结构，会利用后续的 3 篇文章做重点介绍。

---

?四、三元组顺序表，稀疏矩阵的三元组表示及（C语言）实现

本节介绍稀疏矩阵的三元组顺序表压缩存储方式。

通过《矩阵的压缩存储》一节我们知道，稀疏矩阵的压缩存储，至少需要存储以下信息：

• 矩阵中各非 0 元素的值，以及所在矩阵中的行标和列标；
• 矩阵的总行数和总列数；

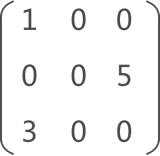
图 1 稀疏矩阵示意图

例如，图 1 是一个稀疏矩阵，若对其进行压缩存储，矩阵中各非 0 元素的存储状态如图 2 所示：

图 2 稀疏矩阵的压缩存储示意图

图 2 的数组中，存储的是三元组（即由 3 部分数据组成的集合），组中数据分别表示（行标，列标，元素值）。

注意，这里矩阵的行标和列标都从 1 开始。

C 语言中，三元组需要用结构体实现，如下所示：

//三元组结构体

typedef struct {

????????int i,j;//行标i，列标j

????????int data;//元素值

}triple;

由于稀疏矩阵中非 0 元素有多个，因此需要建立 triple 数组存储各个元素的三元组。除此之外，考虑到还要存储矩阵的总行数和总列数，因此可以采用以下结构表示整个稀疏矩阵：

#define number 20

//矩阵的结构表示

typedef struct {

????????triple data[number];//存储该矩阵中所有非0元素的三元组

????????int n,m,num;//n和m分别记录矩阵的行数和列数，num记录矩阵中所有的非0元素的个数

}TSMatrix;

可以看到，TSMatrix 是一个结构体，其包含一个三元组数组，以及用于存储矩阵总行数、总列数和非 0 元素个数的变量。

假设采用 TSMatrix 结构体存储图 1 中的稀疏矩阵，其 C 语言实现代码应该为：

#include<stdio.h>

#define number 3

typedef struct {

????????int i,j;

????????int data;

}triple;

typedef struct {

????????triple data[number];

????????int n,m,num;

}TSMatrix;

//输出存储的稀疏矩阵

void display(TSMatrix M);

int main() {

????????TSMatrix M;

????????M.m=3;

????????M.n=3;

????????M.num=3;

????????M.data[0].i=1;

????????M.data[0].j=1;

????????M.data[0].data=1;

????????M.data[1].i=2;

????????M.data[1].j=3;

????????M.data[1].data=5;

????????M.data[2].i=3;

????????M.data[2].j=1;

????????M.data[2].data=3;

????????display(M);

????????return 0;

}

void display(TSMatrix M){

????????for(int i=1;i<=M.n;i++){

????????????????for(int j=1;j<=M.m;j++){

????????????????????????int value =0;

????????????????????????for(int k=0;k<M.num;k++){

????????????????????????????????if(i == M.data[k].i && j == M.data[k].j){

????????????????????????????????????????printf("%d ",M.data[k].data);

????????????????????????????????????????value =1;

????????????????????????????????????????break;

????????????????????????????????}

????????????????????????}

????????????????????????if(value == 0)

????????????????????????????????printf("0 ");

????????????????}

????????????????printf("\n");

????????}

}

输出结果为：

1 0 0
0 0 5
3 0 0